Research at SystemsLab
SystemsLab aims to develop systematic approaches to problems in science, engineering and scientific management. Our research has three primary components: modeling, solution algorithms, and applications to challenging problems.
A list of our sponsors and projects can be found in the Projects page.
Modeling
Propositional Logic:
An important concern in the modeling of complex systems is the expression of interrelationships among the qualitative and/or discrete features of the system. Propositional Logic offers a sound framework for this purpose. Boolean variables are used to establish these interrelationships. A Boolean variable can take discrete values True or False. The following Logical Operators are used:
AND (∧): gives conjunction among different logical clauses. For example: "A∧B" is read as "A and B". Such a conjunction is true if both A and B are true. In all other cases it is false.
OR (∨): gives disjunction among different logical clauses. For example: "A∨B" is read as "A or B". Such a disjunction is false if both A and B are false. In all other cases it is true.
NOT (¬): gives the negation of logical clauses. Logical negation is a unary logical operator that reverses the truth value of its operand. For example: "¬A" is read as "not A". Such a logical clause is false if A is true and true if A is false.
XOR(∨): is also called exclusive disjunction. In a propositional logic statement with two logical clauses connected with xor, the result is true if only one of the operands is true. For example: "A∨B" is read as "A xor B". Such an exclusive disjunction is false if both A and B are false or true. In all other cases it is true.
IMPLICATION(→): is a conditional statement indicating the conditions if the antecedent were true. For example: "A → ¬B" is read as "A implies not B". Such a conditional statement indicates that when A is true, B must be false for this implication to hold. When A is false, no logical inference can be driven from this statement.
EQUIVALENCE(⇔): is a logical operator connecting two clauses to show that both clauses have the same logical content. For example: "A⇔¬B" is read as "A is equivalent to not B". Such an equivalence indicates that when A is true, B must be false and vice versa for this implication to hold. When A is false or B is true, no logical inference can be driven from this statement.
Generalized Disjunctive Programming:
Generalized Disjunctive Programming is a natural framework for modeling complex systems with discrete nature. The mathematical programming problems can be modeled in the Generalized Disjunctive Programming framework as follows:
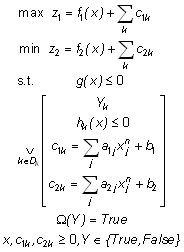
It is possible to have more than one objective function. The objective functions are subject to three types of constraints:
General Constraints: these general algebraic constraints are valid regardless of the discrete nature of the system. They involve only continuous variables x.
Disjunctions: these constraints relate the discrete nature of the system to the physical model given by the constraints hk(x)≤0. These constraints are applicable only when the Boolean variable, Yk, defined for the disjunction k is true. In addition, the costs regarding the discrete nature of the system are given by c1k and c2k that are functions of a subset of variables xj. These costs are valid only when the Boolean variable, Yk, defined for the disjunction k is true; otherwise, they are fixed to 0.
Propositional Logic: These constraints are used to express the interrelationships among the qualitative and/or discrete features of the system.
Sample Publications:
-
Turkay, M., and I.E. Grossmann, "Logic-Based MINLP Algorithms for the Optimal Synthesis of Process Networks", Comput. Chem. Engng., 20, 959-978 (1996). (received 1997 AIChE/CAST Division Ted Peterson Award)
-
Turkay, M., and I.E. Grossmann, "Disjunctive Programming Techniques for the Optimization of Process Systems with Discontinuous Investment Costs-Multiple Size Regions", Ind. Eng. Chem. Res., 35, 2611-2623 (1996).
-
Turkay, M., and I.E. Grossmann, "Tight Mixed-Integer Optimization Models for the Solution of Linear and Nonlinear Systems of Disjunctive Equations", Comput. Chem. Engng., 22, 1229-1239 (1998).
-
Uney, F., and M. Turkay, "A Mixed-Integer Programming Approach to Multi-Class Data Classification Problem", European Journal of Operational Research, in print (2005).
-
Turkay, M., C. Oruç, K. Fujita, and T. Asakura, "Multi-Company Collaborative Supply Chain Management with Economical and Environmental Considerations", Comput. Chem. Eng., 28, 985-992 (2004).
-
Soylu, A., C. Oruc, M. Turkay, K. Fujita, and T. Asakura, "Synergy Analysis of Collaborative Supply Chain Management in Energy Systems using Multi-Period MILP", European Journal of Operational Research, in print (2004).
Solution Algorithms
The solution algorithms for the optimization problems can be tailored depending on the characteristics of the model. An optimization model can exhibit the following variations:
-
Discrete/Continuous: The decision variables and constraints in the model exhibit discrete or continuous behavior. Some or all of the decision variables in an optimization problem can have discrete values (e.g., Boolean Variables: Yes, No, Binary Variables= 0, 1, Integer Variables=0,1,2,...,N). The continuous variables can have any real value at the optimal solution while the discrete variables can have only certain values at any feasible (including the optimal) solution. Therefore, in general obtaining solutions to optimization problems that contains discrete variables is much harder than problems containing continuous variables only. In addition, the constraints can exhibit discrete behavior such as piecewise or conditional constraints. We express such constraints using disjunctions.
-
Linear/Nonlinear: The objective function and the constraints in an optimization problem may involve linear or nonlinear terms. The problems containing only linear terms in the objective function and constraints can be solved relatively easily compared to the ones with nonlinear terms. Nonlinear problems may also contain nonconvex terms that are even more difficult to solve since nonconvex problems have multiple locally optimal solutions. Finding the globally optimal solution for nonconvex problems is a major concern in mathematical programming.
-
Single-Objective/Multi-Objective: Optimization problems are traditionally modeled considering a single objective. However, many real-life problems has a number of objectives that needs consideration. The solution of single-objective optimization problems are easier compared to the multi-objective optimization problems.
-
Certain/Uncertain: The scalars and parameters in the optimization model may have certain fixed values or they can be represented with a distribution or a range of values. The solution of the problems with certain data is easier compared to the ones with uncertain data.
We address solution of discrete-continuous optimization problems with linear and nonlinear terms in the objective functions and constraints.
Sample Publications:
-
Turkay, M., and I.E. Grossmann, "Logic-Based MINLP Algorithms for the Optimal Synthesis of Process Networks", Comput. Chem. Engng., 20, 959-978 (1996). (received 1997 AIChE/CAST Division Ted Peterson Award)
-
Turkay, M., and I.E. Grossmann, "Disjunctive Programming Techniques for the Optimization of Process Systems with Discontinuous Investment Costs-Multiple Size Regions", Ind. Eng. Chem. Res., 35, 2611-2623 (1996).
-
Turkay, M., and I.E. Grossmann, "Tight Mixed-Integer Optimization Models for the Solution of Linear and Nonlinear Systems of Disjunctive Equations", Comput. Chem. Engng., 22, 1229-1239 (1998).
Application Areas
The application areas include process systems engineering, systems biology, and supply chain management and logistics:

